This post presents the asymmetric finite-difference scheme build in staggered grid. This asymmetric scheme works well for processing boundary points.
Wave Modeling in Stratified Media
This post presents wave modeling techniques related to Prof. Kennett’s method. Detailed derivation, and analysis are introduced in the book <
Linear Inversion of Receiver Function
In receiver function inversion, the model is calibrated and the target is to minimize the mismatch between synthetic receiver function waveform and observed waveform. The key point of the inversion is to give a “good” model calibration direction, and amount. In linear inversion, these calibration items are given by the first order derivative of the optimal function. However, it is difficult to derive the analytical expression of the first order derivative since the relationship between model
and receiver function waveform is extreme complex. Finite difference provides approximate value of differential value.
Finite Difference of Staggered Grid (1)
This post presents the central finite difference(FD) system build in stagger grid. Symmetric scheme are derived and examples are presented.
Asymmetric Finite Difference for Boundary Points
For $2i$th order accuracy finite difference(FD), symmetric scheme cannot apply to $i$ boundary points. Thus, asymmetric scheme are required.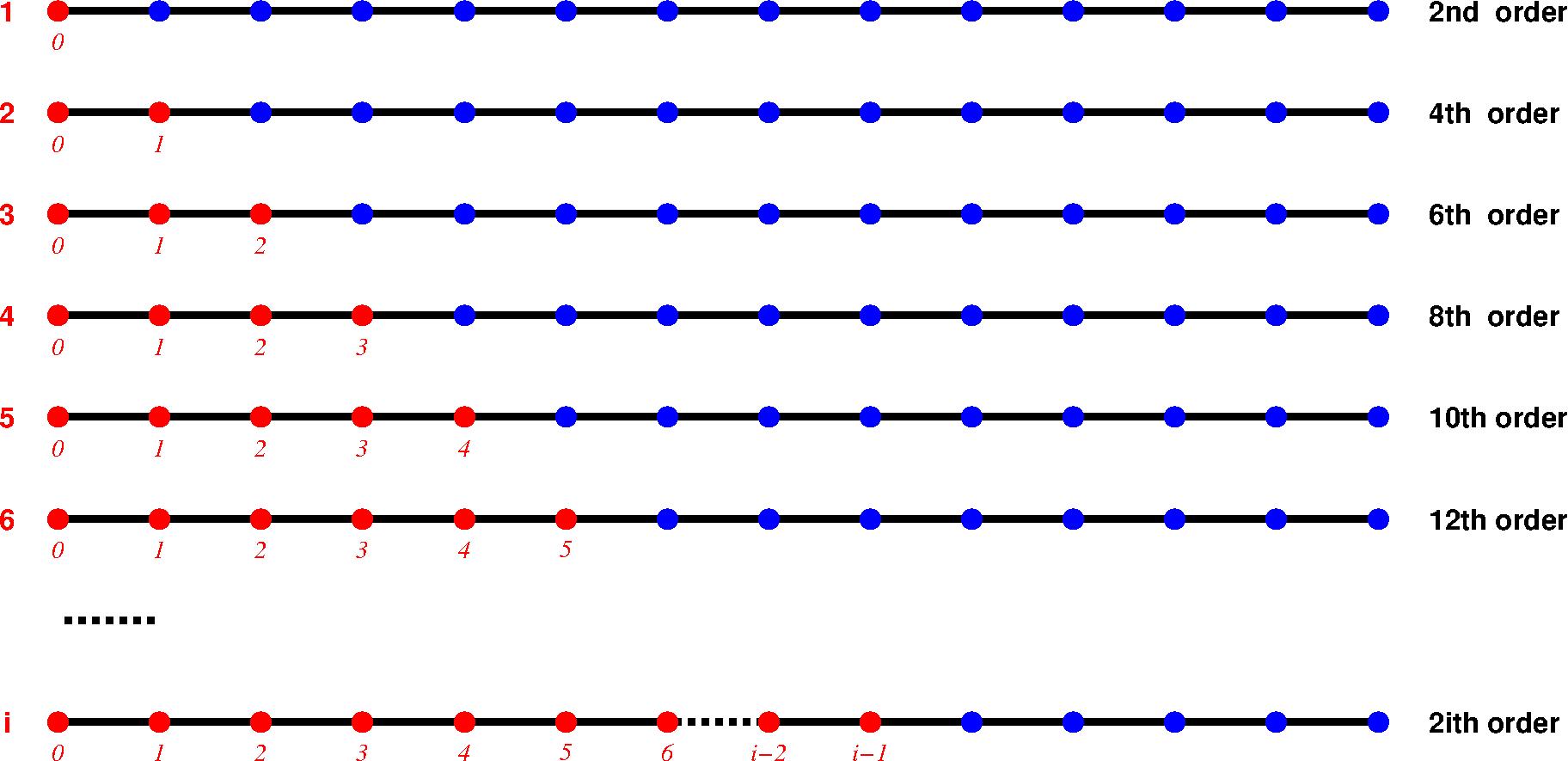
Solving Vandermonde Equation for FD
This post presents how to solve vandermonde equation in finite-difference. For 2N order accuracy finite-difference of derivatives, $C_k(k=1,2,…,N)$ is the solution of a vandermonde equation:
Central Finite Difference of Derivatives(中心有限差分)
This post derived the method of central finite difference for calculating derivatives, especially for first and second order derivatives, and finally arrive at perfect results. Example are provided to verify the results.