Asymmetric Finite Difference for Boundary Points

For $2i$th order accuracy finite difference(FD), symmetric scheme cannot apply to $i$ boundary points. Thus, asymmetric scheme are required.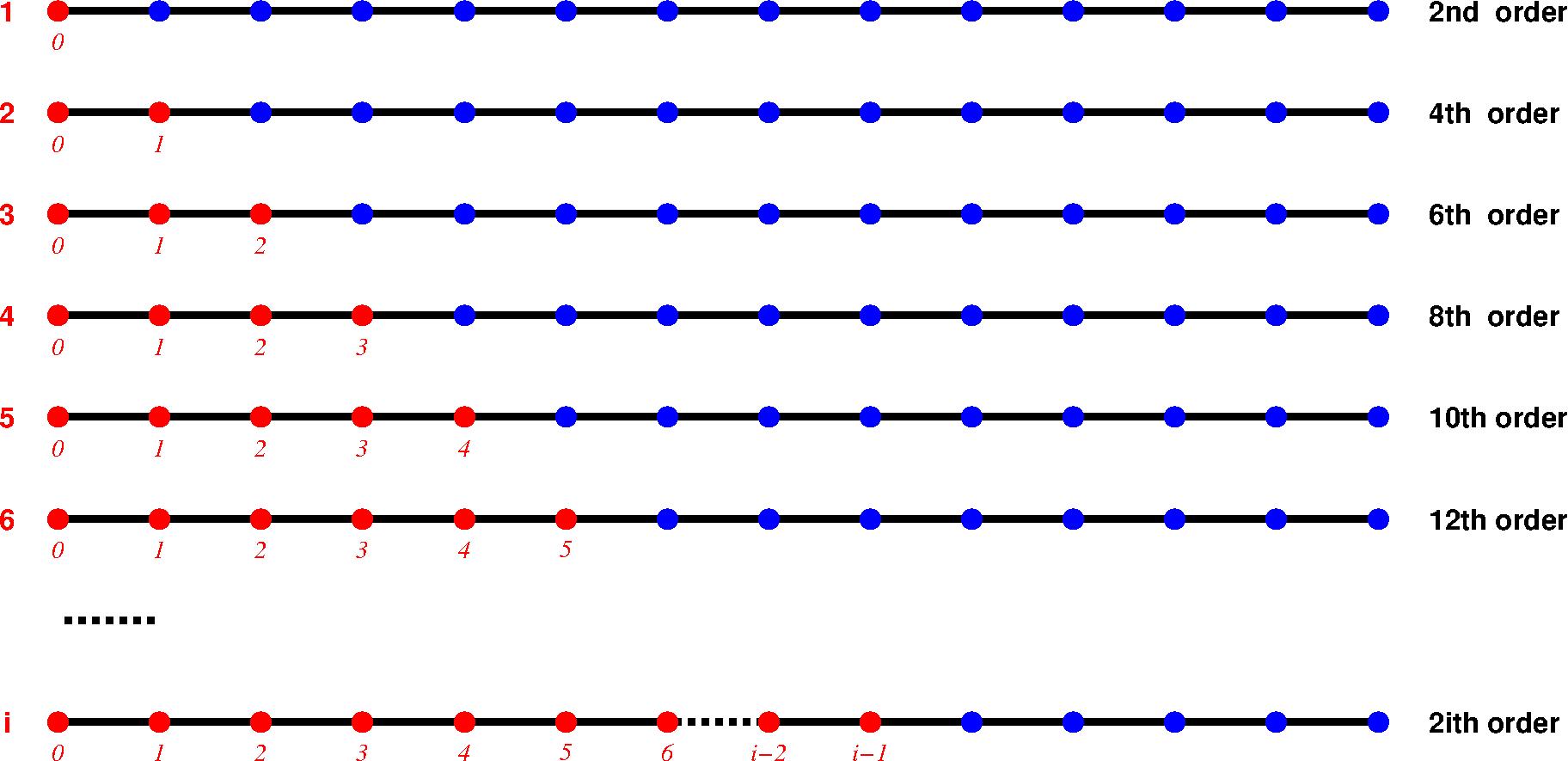

• 2nd order accuracy
  • point 0
• 2ith order accuracy
  • point 0
  • point 1
  • point k (k=0,1,…,i-1)
• Result
• Examples

Let us take 2nd order FD as example:

2nd order accuracy

point 0

$$\begin{eqnarray} f(x) & = & f(x)\\ f(x+\delta ) & = & f(x) + \delta f'(x) + \frac{\delta ^2}{2!} f''(x) + \frac{\delta ^3}{3!} f^{(3)} (x) + ... + \frac{\delta ^n}{n!} f^{(n)} (x) + O(\delta^{n+1})\\ f(x+2\delta ) & = & f(x) + 2\delta f'(x) + \frac{2^2\delta ^2}{2!} f''(x) + \frac{2^3\delta ^3}{3!} f^{(3)} (x) + ... + \frac{2^n\delta ^n}{n!} f^{(n)} (x) + O(\delta^{n+1})\\ \end{eqnarray}$$

Thus, $f’(x)$ is:

$$\begin{eqnarray} f'(x;\delta) & = & \frac{f(x+\delta )- f(x) } {\delta} -\frac{\delta }{2!} f''(x) -\frac{\delta ^2}{3!} f^{(3)} (x) -... -\frac{\delta ^{n-1}}{n!} f^{(n)} (x) +O(\delta^{n})\\ f'(x;2\delta) & = & \frac{f(x+2\delta )- f(x) } {2\delta} -\frac{2\delta }{2!} f''(x) -\frac{2^2\delta ^2}{3!} f^{(3)} (x) -... -\frac{2^{n-1}\delta ^{n-1}}{n!} f^{(n)} (x) +O(\delta^{n})\\ \end{eqnarray}$$

adding $f’(x;\delta)$ and $f’(x;2\delta)$ proportionally:

$$\begin{equation} \begin{cases} \begin{aligned} f'(x) = & C_{21}\frac{f(x+\delta )- f(x) } {\delta} +C_{22}\frac{f(x+2\delta )- f(x) } {2\delta} \\ &-\frac{\delta }{2!}f''(x) \left[ C_{21} + 2C_{22}\right] -... -\frac{\delta^{n-1}}{n!}f^{(n)}(x) \left[C_{21} +2^{n-1}C_{22}\right] +O(\delta^{n})\\ 1 = & C_{21} + C_{22} \end{aligned}\\ \end{cases} \end{equation}$$

Thus, for 2nd order accuracy, item of $\delta$ should be eliminated, so:

$$\begin{equation} \begin{cases} C_{21} + C_{22} & = & 1 \\ C_{21} + 2C_{22} & = & 0 \\ \end{cases} \Rightarrow \begin{cases} C_{21} & = & 2 \\ C_{22} & = & -1 \\ \end{cases} \end{equation}$$

2ith order accuracy

point 0

For point 0, we have:

$$\begin{eqnarray} f(x) & = & f(x)\\ f(x+\delta ) & = & f(x) + \delta f'(x) + \frac{\delta ^2}{2!} f''(x) + \frac{\delta ^3}{3!} f^{(3)} (x) + ... + \frac{\delta ^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ f(x+2\delta ) & = & f(x) + 2\delta f'(x) + \frac{2^2\delta ^2}{2!} f''(x) + \frac{2^3\delta ^3}{3!} f^{(3)} (x) + ... + \frac{2^{2i}\delta ^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ f(x+3\delta ) & = & f(x) + 3\delta f'(x) + \frac{3^2\delta ^2}{2!} f''(x) + \frac{3^3\delta ^3}{3!} f^{(3)} (x) + ... + \frac{3^{2i}\delta ^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ &...&\\ f(x+2i\delta ) & = & f(x) + 2i\delta f'(x) + \frac{(2i)^2\delta ^2}{2!} f''(x) + \frac{(2i)^3\delta ^3}{3!} f^{(3)} (x) + ... + \frac{(2i)^{2i}\delta ^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ \end{eqnarray}$$

Thus, $f’(x)$ is:

$$\begin{eqnarray} f'(x;\delta) & = & \frac {f(x+\delta ) - f(x)}{\delta} -\frac{\delta }{2!} f''(x) -\frac{\delta ^2}{3!} f^{(3)} (x) -... -\frac{\delta ^{2i-1}}{(2i)!} f^{(2i)} (x) +O(\delta^{2i})\\ f'(x;2\delta) & = & \frac {f(x+2\delta ) - f(x)}{2\delta} -\frac{2 \delta }{2!} f''(x) -\frac{2^2\delta ^2}{3!} f^{(3)} (x) -... -\frac{2^{2i-1}\delta ^{2i-1}}{(2i)!} f^{(2i)} (x) +O(\delta^{2i})\\ f'(x;3\delta) & = & \frac {f(x+3\delta ) -f(x)} {3\delta} -\frac{3 \delta }{2!} f''(x) -\frac{3^2\delta ^2}{3!} f^{(3)} (x) -... -\frac{3^{2i-1}\delta ^{2i-1}}{(2i)!} f^{(2i)} (x) +O(\delta^{2i})\\ &...&\\ f'(x;2i\delta) & = & \frac{f(x+2i\delta ) - f(x)}{2i\delta } -\frac{ 2i \delta }{2!} f''(x) -\frac{(2i)^2\delta ^2}{3!} f^{(3)} (x) -... -\frac{(2i)^{2i-1}\delta ^{2i-1}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i})\\ \end{eqnarray}$$

adding $f’(x;\delta), f’(x;2\delta),…,f’(x;2i\delta)$ proportionally:

$$\begin{equation} \begin{aligned} f'(x) = & \sum \limits_{j=1}^{2i} C_{(2i)j} \frac { f(x+j\delta) -f(x) }{j\delta} \\ & - \frac{\delta }{ 2!}f''(x) \sum \limits_{j=1}^{2i}C_{(2i)j}j - \frac{\delta^2 }{ 3!}f^{(3)}(x) \sum \limits_{j=1}^{2i}C_{(2i)j}j^2 - ... - \frac{\delta^{2i-1}}{(2i)!}f^{(2i)}(x)\sum \limits_{j=1}^{2i}C_{(2i)j}j^{2i-1} + O(\delta^{2i})\\ \end{aligned} \end{equation}$$

Thus, for 2ith order accuracy, item of $\delta,\delta^2,…,\delta^{2i-1}$ should be eliminated, so:

$$% \begin{eqnarray} % \begin{cases} % \sum \limits_{j=1}^{2i} C_{(2i)j} = 1 \\ % \sum \limits_{j=1}^{2i} C_{(2i)j}j = 0 \\ % \sum \limits_{j=1}^{2i} C_{(2i)j}j^2 = 0 \\ % ...\\ % \sum \limits_{j=1}^{2i} C_{(2i)j}j^{2i-1} = 0 \\ % \end{cases} % \end{eqnarray}$$ $$\begin{eqnarray} \begin{bmatrix} 1 & 1 & 1 & 1 & ... & 1 \\ 1 & 2 & 3 & 4 & ... & 2i \\ 1 & 2^2 & 3^2 & 4^2 & ... & (2i)^2 \\ ...\\ 1 & 2^{2i-1} & 3^{2i-1} & 4^{2i-1} & ... & (2i)^{2i-1} \\ \end{bmatrix} \begin{bmatrix} C_{(2i)1}\\ C_{(2i)2}\\ C_{(2i)3}\\ ...\\ C_{(2i)(2i)}\\ \end{bmatrix} = \begin{bmatrix} 1\\ 0\\ 0\\ ...\\ 0\\ \end{bmatrix} \end{eqnarray}$$ $$%\begin{eqnarray} % \begin{bmatrix} % 1 & 1 & 1 & 1 & ... & 1 \\ % 1 & 2 & 3 & 4 & ... & N \\ % 1 & 2^2 & 3^2 & 4^2 & ... & N^2 \\ % ...\\ % 1 & 2^{N-1} & 3^{N-1} & 4^{N-1} & ... & N^{N-1} \\ % \end{bmatrix} % \begin{bmatrix} % C_{N1}\\ % C_{N2}\\ % C_{N3}\\ % ...\\ % C_{NN}\\ % \end{bmatrix} % = % \begin{bmatrix} % 1\\ % 0\\ % 0\\ % ...\\ % 0\\ % \end{bmatrix} %\end{eqnarray}$$

point 1

…

point k (k=0,1,…,i-1)

For point k, we have:

$$\begin{eqnarray} f(x-k\delta) & = & f(x) - k\delta f'(x) + \frac{ (-k)^2\delta^2 }{2!} f''(x) + ... + \frac{(-k)^{2i}\delta^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ ...\\ f(x-\delta ) & = & f(x) - \delta f'(x) + \frac{(-1)^2\delta ^2}{2!} f''(x) + ... + \frac{(-1)^{2i}\delta^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ f(x) & = & f(x)\\ f(x+\delta ) & = & f(x) + \delta f'(x) + \frac{\delta ^2}{2!} f''(x) + %\frac{\delta ^3}{3!} f^{(3)} (x) + ... + \frac{\delta ^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ ...\\ f(x+(2i-k)\delta) & = & f(x) + (2i-k)\delta f'(x) + \frac{(2i-k)^2 \delta ^2}{2!} f''(x) + %\frac{(2i-k)^3 \delta ^3}{3!} f^{(3)} (x) + ... + \frac{(2i-k)^{2i}\delta ^{2i}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i+1})\\ \end{eqnarray}$$

Thus, $f’(x)$ is:

$$\begin{eqnarray} f'(x) & = & \frac{f(x-k\delta) - f(x)}{- k\delta } -\frac{ (-k)\delta }{2!} f''(x) - ... -\frac{(-k)^{2i-1}\delta^{2i-1}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i})\\ ...\\ f'(x) & = & \frac{f(x-\delta ) - f(x)}{- \delta } -\frac{-\delta}{2!} f''(x) - ...- -\frac{(-1)^{2i-1}\delta^{2i-1}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i})\\ f'(x) & = & \frac{f(x+\delta ) - f(x)}{\delta } -\frac{\delta}{2!} f''(x) - ... - \frac{\delta ^{2i-1}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i})\\ ...\\ f'(x) & = & \frac{f(x+(2i-k)\delta)-f(x)}{(2i-k)\delta } -\frac{(2i-k) \delta }{2!} f''(x) -... -\frac{(2i-k)^{2i-1}\delta ^{2i-1}}{(2i)!} f^{(2i)} (x) + O(\delta^{2i})\\ \end{eqnarray}$$

adding all these $f’(x)$ proportionally:

$$\begin{equation} \begin{aligned} f'(x) = & \sum \limits_{j=-k}^{2i-k} C^k_{(2i)j} \frac{ f(x+j\delta)-f(x) }{j\delta}\\ &- \frac{\delta}{2!}f''(x) \sum\limits_{j=-k}^{2i-k}jC^k_{(2i)j} - \frac{\delta^2}{3!}f^{(3)}(x) \sum\limits_{j=-k}^{2i-k}j^2C^k_{(2i)j} - ... - \frac{\delta^{2i-1}}{(2i)!}f^{(2i)}(x) \sum \limits_{j=-k}^{2i-k}j^{2i-1}C^k_{(2i)j} \end{aligned} \end{equation}$$

Thus, for 2ith order accuracy, item of $\delta,\delta^2,…,\delta^{2i-1}$ should be eliminated, so:

$$\begin{eqnarray} \begin{bmatrix} 1 & 1 &... & 1 & 1 & ... & 1 \\ -k & -k+1 &... & -1 & 1 & ... & 2i-k \\ (-k)^2 &(-k+1)^2 &... & (-1)^2 & 1^2 & ... & (2i-k)^2 \\ (-k)^3 &(-k+1)^3 &... & (-1)^2 & 1^3 & ... & (2i-k)^3 \\ ...\\ (-k)^{2i-1} & (-k+1)^{2i-1} & ... &(-1)^{2i-1} & 1^{2i-1} & ... & (2i-k)^{2i-1} \end{bmatrix} \begin{bmatrix} C^k_{(2i)(-k)} \\ C^k_{(2i)(-k+1)} \\ C^k_{(2i)(-k+2)} \\ ...\\ C^k_{(2i)(-1)} \\ C^k_{(2i)1} \\ ...\\ C^k_{(2i)(2i-k)} \end{bmatrix} = \begin{bmatrix} 1\\ 0\\ 0\\ ...\\ 0\\ \end{bmatrix} \label{LA} \end{eqnarray}$$

Result

For $2i$th order FD accuracy, the $k$th$(k=0,1,2,…,i-1)$ boundary points, $C^k_{(2i)(j)}$ $(j=-k,-k+1,…,-1,1,…,2i-k)$ is the solution of $\eqref{LA}$, while

$$\begin{equation} \begin{aligned} f'(x) = & \sum \limits_{j=-k}^{2i-k} C^k_{(2i)j} \frac{ f(x+j\delta)-f(x) }{j\delta}\\ \end{aligned} \end{equation}$$

Examples

FD scheme corresponding to accuracy orders of 2,4,6,8,10,12 are implemented to $f(x) = sin(x)$, their FD results are ploted versus theoretical first order derivative of $f’(x) = cos(x)$, as well as their error.