一阶声波方程有线差分模拟

本文介绍了一阶声波方程有限差分模拟，并利用一维模型例子加以说明。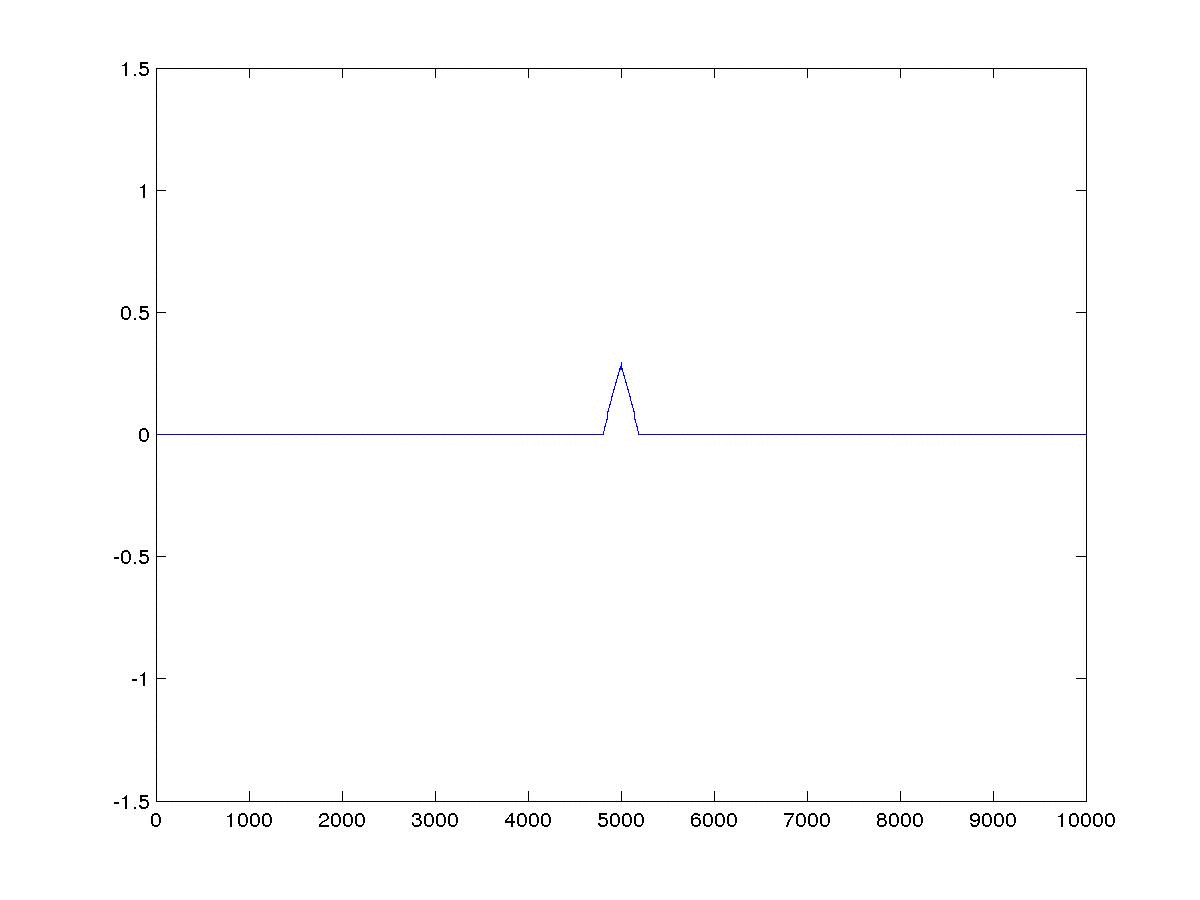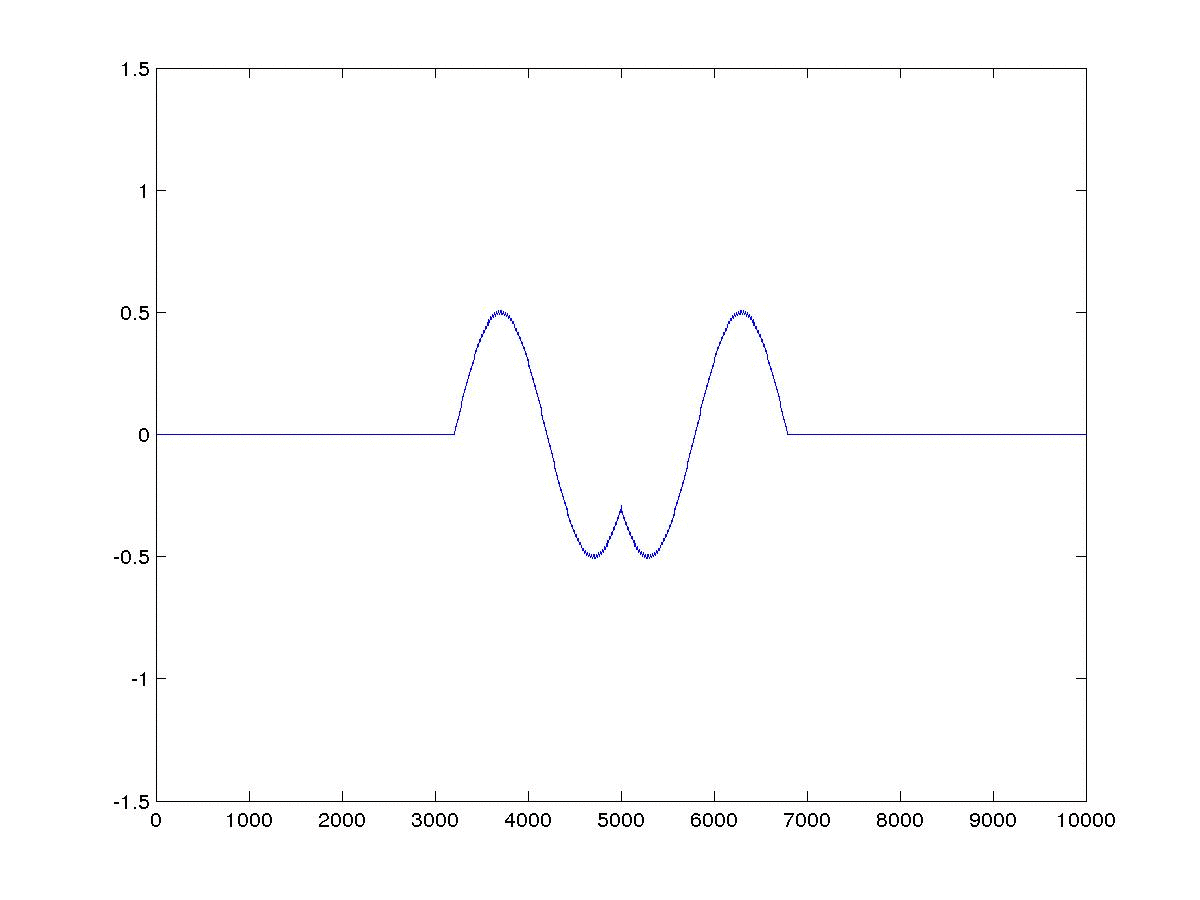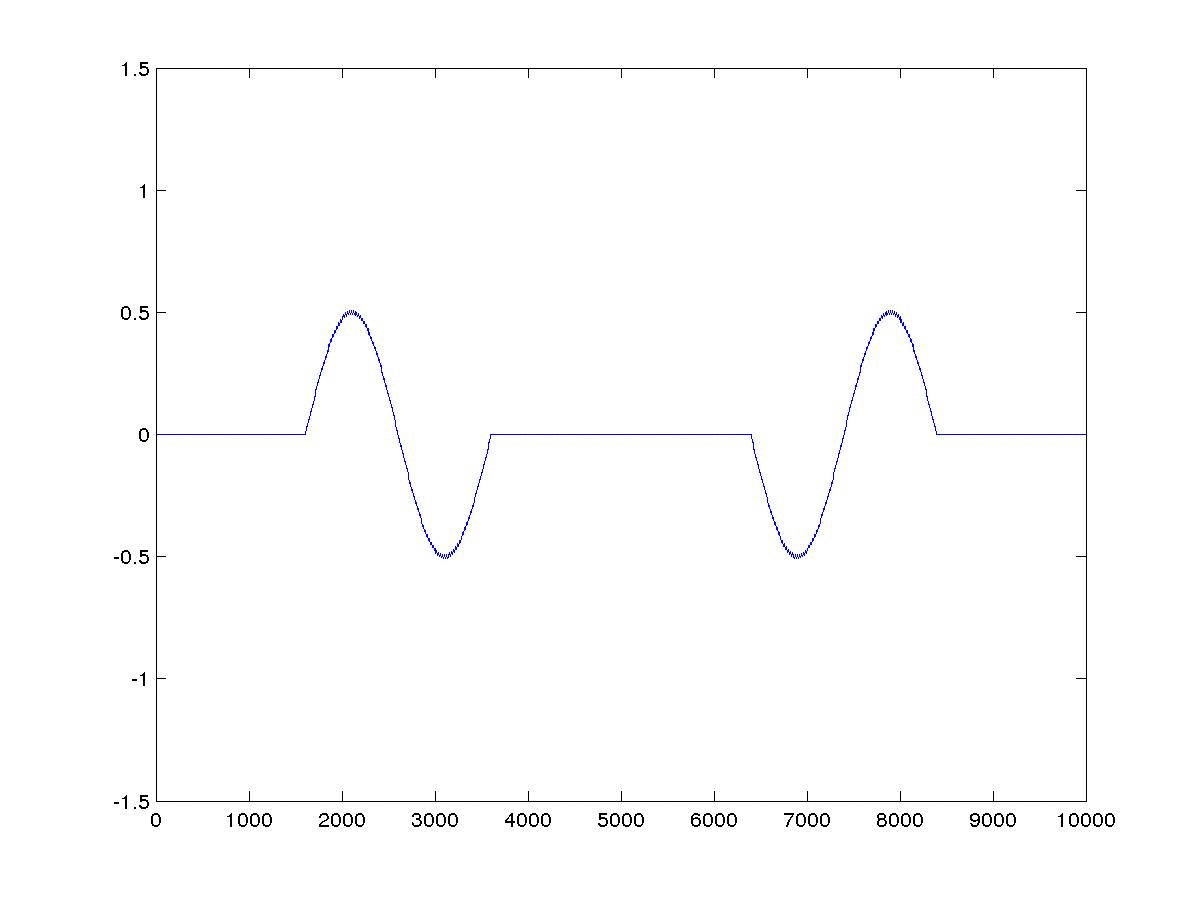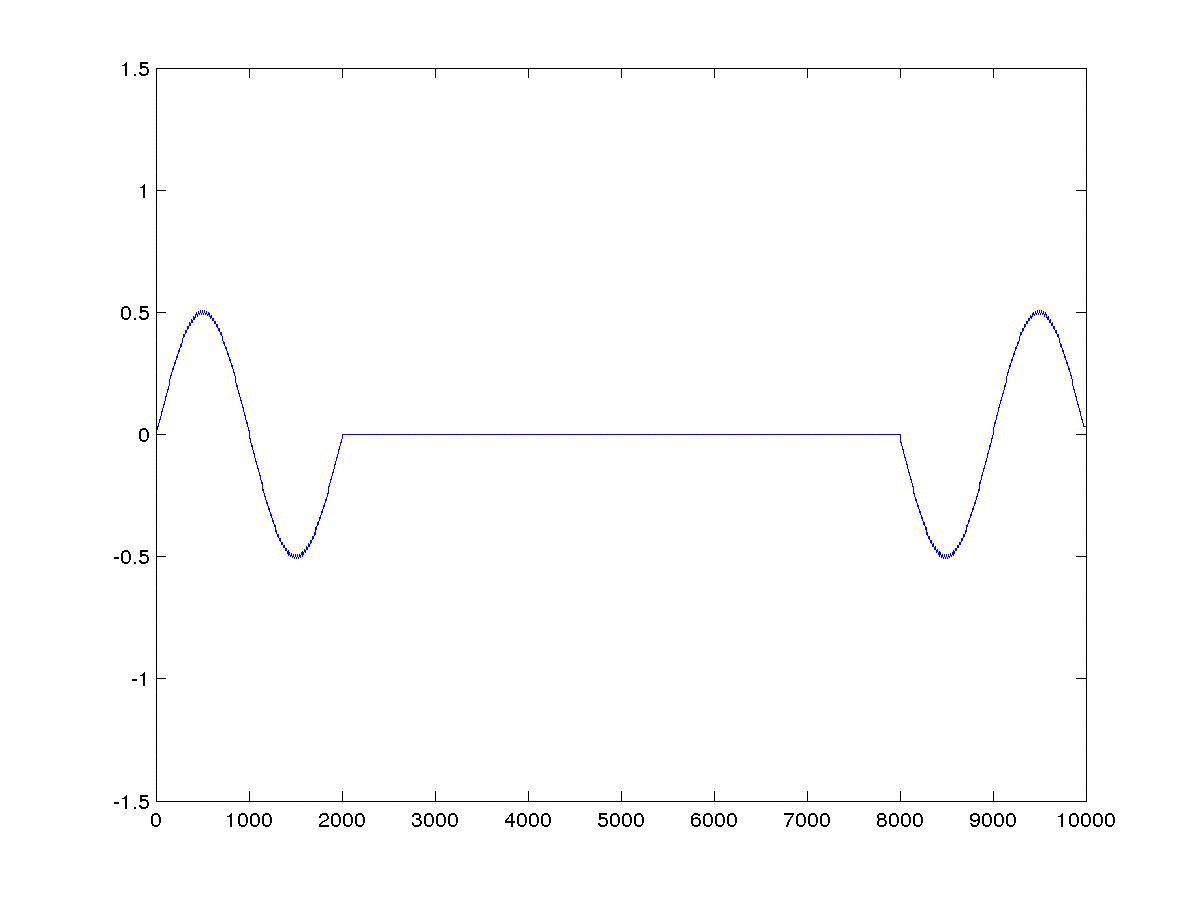

• 控制方程
• 交错网格
• 实现
• 参考文献

控制方程

一维空间下，一阶声波方程可以写成以下形式：$ $

$$\begin{eqnarray} \begin{cases} \frac{\partial p }{\partial t} & = & -\rho v^2\frac{\partial q}{\partial x} + f\\ \frac{\partial q }{\partial t} & = & -\frac{1}{\rho} \frac{\partial p}{\partial x} + q_0 \end{cases} \end{eqnarray}$$

在无外力作用无信号输入情况下，声波方程及其差分形式为：

$$\begin{eqnarray} \begin{cases} \frac{\partial p }{\partial t} & = & -\rho v^2\frac{\partial q}{\partial x}\\ \frac{\partial q }{\partial t} & = & -\frac{1}{\rho} \frac{\partial p}{\partial x} \end{cases} \end{eqnarray}$$ $$\begin{eqnarray} \begin{cases} D_t p_B & = & - \rho v^2 D_x q_B \\ D_t q_A & = & -\frac{1}{\rho}D_x p_A \end{cases} \end{eqnarray}$$

交错网格

参考Virieux(1984, 1986)，构建交错网格如下：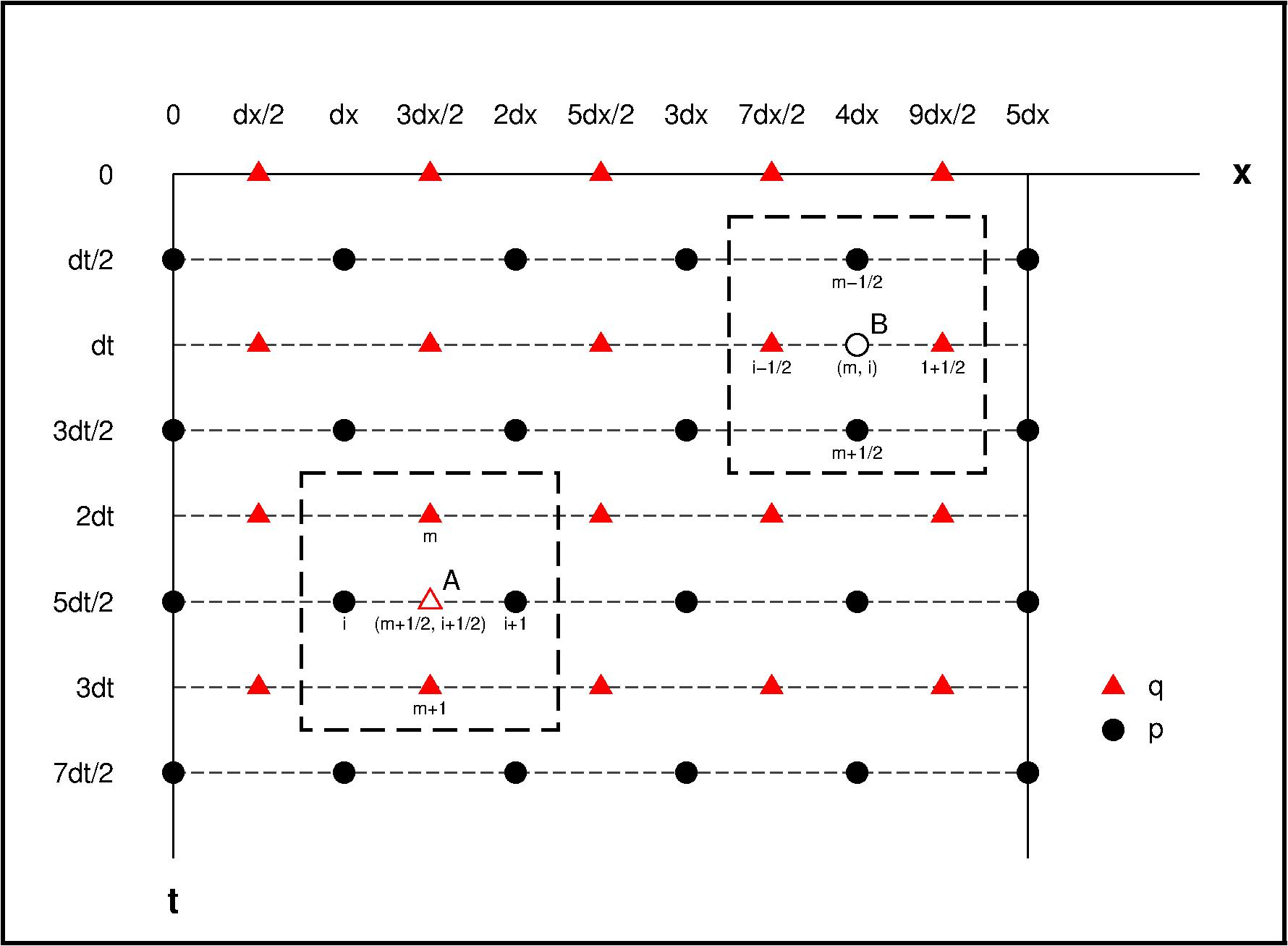

在二阶差分精度下，对于Ｂ点可以推导：

$$\begin{eqnarray} D_t p_B & = & - \rho v^2 D_x q_B \\ \Rightarrow \frac{1}{\Delta t} [ p(x_i, t_{m+1/2}) - p(x_i, t_{m-1/2}) ] & = & -\frac{\rho v^2}{\Delta x} [ q(x_{i+1/2}, t_m) - q(x_{i-1/2}, t_m) ] \end{eqnarray}$$ $$\begin{eqnarray} \Rightarrow p(x_i, t_{m+1/2}) & = & p(x_i, t_{m-1/2}) - \frac{\rho v^2 \Delta t}{\Delta x} [ q(x_{i+1/2}, t_m) - q(x_{i-1/2}, t_m) \end{eqnarray}$$

同样的，可以推导Ａ点：

$$\begin{eqnarray} D_t q_A & = & -\frac{1}{\rho}D_x p_A \\ \Rightarrow \frac{1}{\Delta t} [q(x_{i+1/2},t_{m+1})- q(x_{i+1/2},t_{m}) ]& = & -\frac{1}{\rho \Delta x} [p(x_{i+1}, t_{m+1/2}) - p(x_i, t_{m+1/2})] \end{eqnarray}$$ $$\begin{eqnarray} \Rightarrow q(x_{i+1/2},t_{m+1}) & = & q(x_{i+1/2},t_{m}) -\frac{\Delta t}{\rho \Delta x} [p(x_{i+1}, t_{m+1/2}) - p(x_i, t_{m+1/2})] \end{eqnarray}$$

故而，波场递推关系为：

$$\begin{equation} \begin{cases} q(t=0) \\ p(t=\Delta t/2) \end{cases} \Rightarrow \color{red}{q(t=\Delta t)} \\\Rightarrow \begin{cases} \color{red}{q(t=\Delta t)} \\ p(t=\Delta t/2) \end{cases} \Rightarrow \color{blue}{p(t=3\Delta t/2)} \\\Rightarrow \begin{cases} \color{red}{q(t=\Delta t)} \\ \color{blue}{p(t=3\Delta t/2)}\\ \end{cases} \Rightarrow \color{green}{q(t=2\Delta t)} \\\Rightarrow \begin{cases} \color{green}{q(t=2\Delta t)} \\ \color{blue}{p(t=3\Delta t/2)} \end{cases} \Rightarrow ............\\ ... \end{equation}$$

实现

% Matlab
clear;close all; clc
nx = 1000;   dx  = 10; x = (0:nx-1) * dx;
nt = 2500;   dt  = 1.0e-2;
v  = 1000.0; rho = 1500;

f_wave = 0.5*2.0 * pi ;
n_stop = floor( 2.0 * pi / f_wave   / dt );
src= [ sin( (0:n_stop)*dt*f_wave) zeros(1,nt) ]; %source

p  = zeros(2,nx); q  = zeros(2,nx-1); %initial conditions
new = 1; old = 2;
c_q = -1.0*dt/rho/dx; c_p = -1.0*rho*v*v*dt/dx;
figure
for it = 1:nt
    %  1   2   3   4   5  ...
    %--q---q---q---q---q--...
    %p---p---p---p---p---p...
    %1   2   3   4   5   6...
    p(old,501) = src(it)+p(old,501);
    for ix = 1:nx-1
        q(new,ix) = q(old,ix) + c_q * ( p(old,ix+1) - p(old,ix) );
    end
    for ix = 2:nx-1
        p(new,ix) = p(old,ix) + c_p * ( q(new,ix) - q(new,ix-1) );
    end

    p(new,nx) = p(new,nx-1); % free boundary
    p(new,1)  = p(new,2);
    %p(new,nx) = 0.0; % rigid boundary
    %p(new,1)  = 0.0;
    plot(x,p(old,:));
    axis( [0 nx*dx -1.5 1.5] );
    pause(0.001);
    tmp = old; old = new; new = tmp;
end

参考文献

Virieux J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11): 1933-1942.
Virieux J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901.